请先阅读说明。

Basis of Algorithm Analysis

Rules of O(n) Syntax

  1. Definition: $T(N) = O(f(N))$ if there are positive constants $c$ and $n_0$ such that $T(N) \leq c\times f(N)$ when $N \geq n_0$. Use the tightest one in the course. e.g. $2N^2 = O(N^2)$
  2. If $T_1(N) = O(f(N))$ and $T_2(N) = O(g(N))$, then
    1. $T_1(N) + T_2(N) = \max(O(f(N)),O(g(N)))$
    2. $T_1(N) \times T_2(N) = O(f(N)\times g(N))$
  3. 如果 $T(N)$ 是 k 阶多项式, $T(N) = O(N^k)$
  4. $\log^k(N) = O(N)$ for any constant $k$.

以下复杂度依次递增：

$2/N < 1 < N^{1/2} < N < N\log(\log(N)) < N\log(N)$

$= N\log(N^2) < N\log^2N < N^{1.5} < N^2 < N^2\log(N) < N^3 < 2^{N/2} < 2^N$

General Rules for Algorithm Analysis

  1. For loops: Number of statements $\times$ number of iterations
  2. Nested loops: Number of statements $\times$ loop1 $\times$ loop2 …
  3. Consecutive statements: Add them all.
  4. If/else statement: $\max(\text{if statement, else statement})$

如果有函数调用，先计算被调用函数的复杂度。

Primary Examples of Algorithm

Fibonacci Sequence

递归法：

1
2
3
4
5
6
7
8
int FIB(int n){
    if(n == 1 || n == 2){
        return 1;
    }
    else{
        return FIB(n-1)+FIB(n-2);
    }
}

迭代法

1
2
3
4
5
6
7
8
9
10
11
int FIB(int n){
    int prev1 = 1, prev2 = 1;
    int curr = 2, temp;
    while(curr < n){
        temp = prev1 + prev2;
        prev1 = prev2;
        prev2 = temp;
        curr ++;
    }
    return prev2;
}

迭代法数列形式

1
2
3
4
5
6
7
8
int * FIB_arr_loop(int n){
    int Fib_arr[1000] = {1,1};
    int i;
    for(i = 2; i < n; i++){
        Fib_arr[i] = Fib_arr[i-1] + Fib[i-2];
    }
    return Fib_arr;
}

Maximum Subsequence Sum Problem

Exhaustive Strategy

1
2
3
4
5
6
int max = a[0];
for(int i = 0; i < n; i++){
    for(int j = i; j < n; j++){
        // Sum a[i] to a[j] and update max;
    }
}

Optimized Exhaustive Strategy

穷举法中，可以有 $\sum \limits_{k=i}^j a[k] = \sum \limits_{k=i}^{j-1} a[k] + a[j]$

1
2
3
4
5
6
7
8
int max = a[0];
for(int i = 0; i < n; i++){
    int this_sum = 0;
    for(int j = i; j < n; j++){
        this_sum += a[j];
        max = max > this_sum ? max : this_sum;
    }
}

Divide-and-Conquer

思路：最大子串和只存在三种可能

  1. 只存在于左边一半中
  2. 只存在于右边一半中
  3. 它穿过了中间，存在于左右两半中

解决方案：

  1. Base case: 左半/右半只有 1 个或 0 个元素。
  2. 对于任何 N > 1 元素的序列，将其划分为两半。
  3. 计算左半/右半的最大和，和跨过中间的子串的最大和。
    • 跨过中间的子串的最大和算法：
1
2
3
4
5
6
7
8
9
10
11
int LeftBorderSum = 0, RightBorderSum = 0;
int MaxLeftBorderSum, MAXRightBorderSum;
for(int i = center; i >= left; i--){
    LeftBorderSum += A[i];
    // Update MaxLeftBorderSum
}
for(int i = center; i <= left; i++){
    RightBorderSum += A[i];
    // Update MaxRightBorderSum
}
return MaxLeftBorderSum + MaxRightBorderSum;
  1. 在以上三种情况中选择最大的，就是此串的最大子串和。

The Best Algorithm

思路：如果一个子串的和 < 0，那它一定不是最后的最大子串和的前缀。因此只需要扫描一遍数组，如果某一段的和为负数，就直接将其忽略，从下一个元素开始计算。（同时更新全局最大子串和）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int this_sum = 0, max_sum = 0;
int i = 0, best_i = 0, best_j = 0;
for(int j = 0; j < n; j++){
    this_sum += a[j];
    if(this_sum > max_sum){
        max_sum = this_sum;
        best_i = i;
        best_j = j;
    }
    else if(this_sum < 0){
        i = j + 1;
        this_sum = 0;
    }
}
return max_sum;

适用于已经排序的数组。

  1. 比较数组中间元素与目标的大小
  2. 如果中间元素较大，就在左子串中寻找；如果中间元素较小，就在右子串中寻找。（假设升序，降序亦然）

Abstract Data Type (ADT)

List

Array Implementation

1
2
3
4
5
struct{
    int number;
    char name[20];
    double score;
} Array_List[20];

优势：

  • 易于理解
  • 易于实现
  • 易于随机访问
    • 访问任意元素复杂度 O(1)
    • 更新任意元素复杂度 O(1)

劣势：

  • 浪费空间
  • 难以重新组织元素
    • 插入元素复杂度 O(n)
    • 删除元素复杂度 O(n)

Linked List

优势：

  • 易于更新元素（插入/删除）
  • 不需要提前分配空间

劣势：

  • 难以实现
  • 无法实现随机访问
  • 需要额外的空间分配给指针

Doubly Linked List

在链表的基础上为每一个节点增加一个指向前序节点的指针。

Costs:

  • 增加了空间需求
  • 增加了插入和删除时需要处理的指针数量

Benefits:

  • 将删除元素的时间复杂度降为 O(1)
  • 简化反向遍历

Circularly Linked List

将链表首尾相连。

Stack

Definition: a list with the restriction that insertions and deletions can be performed only at the top. The base of a stack is not allowed to operate directly.

LIFO, last in first out.

Fundamental operations:

  • Top: get the value of the top cell
  • Push: insert on the top
  • Pop: delete the top

Linked List Implementation

基础的链表实现，将 header 所指的对象认为是 top，所有的操作只能够对 header 所指向的 node 进行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
struct Node{
    int element;
    PtrToNode next;
}

typedef struct Node * PtrToNode;
typedef PtrToNode Stack;

// Asserting s is not empty.

int Top(Stack s){
    return s->next->element;
}

void Push(int x, Stack s){
    PtrToNode tmp;
    // malloc space for tmp and fill in the element x
    tmp->next = s->next;
    s->next = tmp;
}

void Pop(Stack s){
    PtrToNode first = s->next;
    s->next = s->next->next;
    free(first);
}

另外，置空 Stack 是通过反复调用 Pop 完成的。

Array Implementation

实现方法：

  1. 声明一个数组 stack[MaxSize]
  2. 声明 int TopOfStack 作为 cursor
  3. TopOfStack == -1 表示堆栈是空的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
struct StackRecord{
    int capacity;
    int top;
    int * array;
}

typedef struct StackRecord * Stack;

// Asserting s is neither full nor empty.

int Top(Stack s){
    return s->array[s->top];
}

void Push(int x, Stack s){
    s->top ++;
    s->array[s->top] = x;
}

void Pop(Stack s){
    s->top --;  // No need to clean the top cell.
}

另外，置空 Stack 只需要直接将 s->top = -1, 无需对数组进行任何操作。

Application: Maze Solving

解决方案：

  1. 访问(1,1)，即 Push(1,1).
  2. 对于访问到的每个位置，如果它就是出口，那么问题解决。如果不是，那就依次尝试访问上下左右四个紧邻的位置。
  3. 如果被尝试访问的紧邻位置 P 满足以下两个条件就 Push§，否则跳过
    1. 不是墙
    2. （全局）从未被访问过
  4. 如果当前 Stack 顶部的位置 Q 的四个方向都被尝试过无法访问，那就 Pop(Q)，并尝试访问 Pop 后 Stack 顶部的位置的下一个方向。
  5. 如果 Stack 最终为空，则没有可行路径。

Queue

Fundamental operations:

  • Enqueue: inserts an element at the rear of the list.
  • Dequeue: deletes (and returns) the element at the front of the list.

FIFO, first in first out.

Circular Array Implementation

实现方法：

  1. 声明一个数组 queue[MaxSize]
  2. 声明 int front, rear, size 来记录信息
  3. 将数组在逻辑上首尾相连
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
struct QueueRecord{
    int capacity;
    int front;
    int rear;
    int size;
    int * array;
}

typedef struct QueueRecord * Queue;

// Asserting q is neither full nor empty.

int Succ(int position, Queue q){
    if(++position == q->capacity){
        position = 0;
    }
}

void Enqueue(int x, Queue q){
    q->size++;
    q->rear = Succ(q->rear,q);
    q->array[q->rear] = x;
}

int Dequeue(Queue q){
    int x = Front(q);
    q->size--;
    q->front = Succ(q->front,q);
}

Application: Maze Solving - FloodFill Algorithm

洪水算法的本质是一个树形结构，通过逐步向外遍历迷宫的方式，使得存储信息的树上第 i 层上有所有第 i 步可以到达的节点。这个算法能够找到迷宫的最短路径。

利用 Queue 来实现树的遍历与保存。

Queue 中每个 cell 保存的信息：

  • index: 这个 cell 在整个队列中的序号
  • position: cell 中位置的坐标
  • pre: 到达这个位置的前一步位置的 cell 所在队列中的序号

注意此时的队列不是循环的，大小是 $m\times n$，Dequeue 之后不清除前面的信息，最后检索整个路径时需要回溯。

解决方案：

  1. Enqueue 起点
  2. Dequeue 并且获得 Front，记为 P. 测试它可以走的各个方向上的位置，如果这个位置 Q 既没有被访问过，也不是墙，就 Enqueue(Q)，注意记录此时的 pre 为 P 的 index
  3. 反复 2 直到：
    1. 找到终点，通过不断跟踪 pre 找到整条路径
    2. 队列为空时仍然没有找到终点，则没有任何可能的路径

Binary Trees

Definition: a tree in which a node can have 0, 1 or 2 children.

二叉树的深度：

  • Worst case: $N - 1$
  • Best case: $O(\log(N))$
  • Average case: $O(\log(N))$ ~ $O(N^{1/2})$

Implementation:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
typedef struct TreeNode * PtrToNode;
typedef PtrToNode Tree;

struct TreeNode{
    int element;
    Tree left;
    Tree right;
}

int Height(Tree t){
    if(t == NULL){
        return -1;
    }
    else{
        return 1 + max(Height(t->left),Height(t->right));
    }
}

Tree Traversal

四种遍历树的方式：

  • Inorder 中序遍历
    • Left sub-tree → (Node) Data → Right sub-tree
  • Postorder 后序遍历
    • Left sub-tree → Right sub-tree → (Node) Data
  • Preorder 后序遍历
    • (Node) Data → Left sub-tree → Right sub-tree
  • Level-order 层次遍历
    • 广度优先，先遍历所有 D 深度的节点，再遍历 D + 1 深度的节点
1
2
3
4
5
6
7
void Inorder(Tree t){
    if(t != NULL){
        Inorder(t->left);
        Visit(t->element);
        Inorder(t->right);
    }
}

Postorder and Preorder are similar.

层次遍历需要使用一个队列来完成。

解决方案：

  1. 声明一个和节点数同样大小的 Queue, 以及游标 rear, front
  2. Enqueue 根节点
  3. Dequeue 并且获取 front, 访问 front 的元素，并且 Enqueue 此时 front 的所有子节点
  4. 反复进行 (3) 直到队列为空为止

Threaded Binary Tree

想法：任意 N 个节点的树中都有 N+1 个空指针，将这些空指针指向其前驱或后继，以提高遍历的效率。需要创建额外的变量来表达某个指针是线索还是子节点。

以中序线索二叉树（需要做中序遍历的二叉树）为例： 实现方法：

  • 如果节点没有左子节点，让其左指针指向其中序访问时的前驱
  • 如果节点没有右子节点，让其右指针指向其中序访问时的后继

例如对于下左二叉树，中序遍历的顺序为 B → D → C → A → E, 因此将其线索化为下右图   

进行中序线索化时，需要一个全局变量来记录全局的前驱后继，以修改节点的空指针。

Binary Search Tree

特性：

  • 每一个节点的值是不相同的。
  • 每个节点左子树上所有节点的值都小于该节点。
  • 每个节点右子树上所有节点的值都大于该节点。

基本操作：

  • MakeEmpty(): 采用后序遍历，free 每个节点
  • Find(): 类似二分查找
  • FindMin(): 找到整棵树最左侧的节点
  • FindMax(): 找到整棵树最右侧的节点
  • Insert(): 在树 t 中插入元素 x
    1. Find(x,t)
    2. 如果 x 被查找到，结束。（每个节点值不同，不能重复插入）
    3. 否则，将 x 插入到查找过程中遍历的最后一个节点的子节点，注意比较大小。
    • x 将永远被作为一个 leaf（没有后继节点）
  • Delete(): 在树 t 中删除元素 x
    1. Find(x,t), 记为节点 P
    2. 如果 P 是一个 leaf，直接删除
    3. 如果 P 只有一个子节点 Q, 无论 Q 是左/右子节点，都直接将 P 的父节点指向 P 的指针指向 Q
    4. 如果 P 有两个子节点 M, N （分别为左，右）:
      1. 将 P 上的元素替换为 N 和 N 的所有子节点中最小的元素 FindMin(N), 记为 O
      2. 删除 O，此时 O 必然没有左子节点，因此化归到 (2) 或者 (3) 的情况

当所有节点都只有一个子节点（除了最后一个节点）时，实际上成为了 List, 各种操作的复杂度会上升为 $O(N)$

AVL Tree

Definition: A Binary Search Tree with restriction: For every node in the tree, the height of its left and right sub-trees can differ by at most 1.

  • The height of an empty tree is -1.
  • The height of an one-node tree is 0.

Insertion and Rotation

在 BST 的插入节点操作之后，可能会使 AVL Tree 不再平衡，这里就需要引入旋转操作来保持平衡。

某个节点 I (Imbalanced) 不满足平衡条件的四种情况：

  1. I 的左子节点 L 的左子树中插入了节点 X，"/"
  2. I 的左子节点 L 的右子树中插入了节点 X，"<"
  3. I 的右子节点 R 的左子树中插入了节点 X，">"
  4. I 的右子节点 R 的右子树中插入了节点 X，"\"

注意虽然插入某个节点 X 这一操作的“瞬间”会影响从 X 到根节点的所有节点，改变其左右子树高度差，但调整是从下向上回溯的。 从插入的节点向上更新高度和高度差，将第一个不平衡的节点记为 I, I 本身会先进行旋转调整保持自身平衡，此时其高度不变，因此其所有父节点的左右子树高度差不变，不会发生旋转。

另外，这里声明一个老师 PPT 上没有的“轴”的概念便于理解。它从图上看是每次旋转发生的轴，同时也是被调整的树完成调整后的根节点，记为 A(Axis).

Single Rotation

适用于 case 1 & 4, 即"/“和”\“的情况。这里仅以”/"情况为例，另一侧为镜像。

这张图表示得非常清楚，5 对应 I, 3 对应 L, 1 插入的位置是在 3 的左子树。此时 A == L.

旋转时发生的事件：

  1. I 的左指针指向 A 的右指针
  2. A 的右指针指向 I
  3. 【图中未显示】将原先 I 的父节点指向 I 的指针现在指向 A。
    • 例如上图中原先 5 可能是 7 的左子节点，那么在旋转完成后，7 的左指针指向 3，并且 7 和以上级别的节点不需要进行调整，因为现在以 3 为根节点的子树的深度和插入前没有变化
    • 这个指针的说法很繁琐，可以用“返回 A”来代替。将事件看作：对于 I 的父节点 U(unaffected) 而言，其左子树(I)中发生的一切都是在黑箱中完成的，U 只需要接收黑箱输出的一个节点作为其左子节点即可，而“返回 A”就是这个黑箱输出 A.

另外，如果图中 2 和 4 不存在，即 3 的右节点是 NULL，1 直接是 3 的左节点，则以上描述的步骤仍然完全相同。

Double Rotation

适用于 case 2 & 3, 即"<“和”>“的情况。这里仅以”<"情况为例，另一侧为镜像。

仍然注意 50 对应 I, 40 对应 L, 47 插入的位置是在 L 的右子树。这里 A 是 L 的右子节点。

旋转时发生的事件：

  1. 对 A 进行向左的单旋转
    1. L 的右指针指向 A 的左子节点（这里是 NULL）
    2. A 的左指针指向 L
    3. 返回 A
  2. 对 A 再进行一次向右的单旋转
    1. I 的左指针指向 A 的右子节点
    2. A 的右指针指向 I
    3. 返回 A
  3. 最终返回 A

双旋转就是两个方向的两次单旋转而已。

  • case 2 - “左子节点右子树”，单旋转先向左再向右
  • case 3 - “右子节点左子树”，单旋转先向右再向左

Deletion

这一部分在老师的 PPT 上完全没有提到，全部由自己的思考完成，可能有误。

实现方案：

  1. 首先进行正常的删除操作。
  2. 从被删除的节点开始向上回溯检查是否存在不平衡，找到不平衡的节点。
  3. 对于该不平衡的节点 I ，其不平衡的原因有两种情况（以下记 L 为 I 的左子树，R 为 I 的右子树：
    1. 类似于插入时四种情况：
      1. L 的高度比 R 的右子树少 1，即"\"
      2. L 的高度比 R 的左子树少 1，即">"
      3. R 的高度比 L 的右子树少 1，即"<"
      4. R 的高度比 L 的左子树少 1，即"/"
    2. 其中一方的两个子节点具有同样的高度：
      1. L 的高度比 R 的两颗子树都少 1
      2. R 的高度比 L 的两颗子树都少 1

显然其中一半的状况是对称的，因此只讨论另一半状况。

【灵魂画手上线】

假设 L 在删除前存在一个子节点，此时 I 是平衡的，删除的对象是 L 的子节点，此后产生不平衡。 对于第一种和第二种情况，分别直接按照插入时对于 “>” 和 "\"的处理方法，进行 Double Rotate 和 Single Rotate 就可以完成。 对于第三种情况，检验发现直接以 R 为轴进行 Single Rotate，可以直接恢复平衡。

与插入不同的是，删除某一个节点引起的树的调整，可能让该树的高度减小，而并非如插入那样调整后能保证不变。因此一次删除可能会造成全局层面多颗子树的调整。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
AvlTree Delete(int x, AvlTree t)
{
	Position tmp;
	if (t == NULL) {
		printf("Element not found.\n");
		return NULL;
	}
    // Start locating x
	else if (x < t->element) {
		t->left = Delete(x, t->left);
		t->height = 1 + MaxSubTreeHeight(t);    // Remember to update the height.
	}
	else if (x > t->element) {
		t->right = Delete(x, t->right);
		t->height = 1 + MaxSubTreeHeight(t);
	}
	else {
    // Finish locating t, now t->element == x
    // Start processing the standard deleting procedure.
		if (t->left && t->right) {  // Case when the element to be deleted has two nodes.
			tmp = FindMin(t->right);
			t->element = tmp->element;
			t->right = Delete(t->element, t->right);
		}
		else {  // Case when the element to be deleted has one node.
			tmp = t;
			if (t->left == NULL) {
				t = t->right;
			}
			else if (t->right == NULL) {
				t = t->left;
			}
			free(tmp);
		}
	}
    // Finish standard deleting procedure.
    // Start adjusting.
	if (t != NULL && IntervalBetweenSubHeight(t) == 2) {    // If t is unbalanced
		if (Height(t->left) > Height(t->right)) {   // If L is deeper than R, resembling "/" or "<" in insertion case.
			if (t->left->left == NULL && t->left->right != NULL) {  // Case "<"
				t = DoubleRotateWithLeft(t);
			}
			else {  // Case "/"
				t = SingleRotateWithLeft(t);
			}
		}
		else {  // If R is deeper than L, resembling "\" or ">" in insertion case.
			if (t->right->right == NULL && t->right->left != NULL) {    // Case ">"
				t = DoubleRotateWithRight(t);
			}
			else {  // Case "\"
				t = SingleRotateWithRight(t);
			}
		}
	}
	if (t != NULL) {
		t->height = 1 + MaxSubTreeHeight(t);    // Updating height.
	}
	return t;
}

Sorting

对于 N 个元素进行排序，这些元素当前存储在大小为 N 的数列内部。

  • Internal Sorting （内部排序）：数据量较小，可以直接读取到内存中进行处理
  • Expernal Sorting （外部排序）：数据量过大，无法直接读取到内存中，需要与外部存储进行 I/O

此部分的复杂度分析相对重要，见所有复杂度汇总表格

BST-Based Sorting

步骤：

  1. 用数据构造一颗 BST
  2. 进行 Inorder 遍历并且输出

Naive Strategy - Straight Selection Sort

步骤：

  1. 扫描整个数列，找到最小元素
  2. 将其与数列的第一个元素进行交换
  3. 对数组的剩余部分重复以上步骤

Insertion Sort

  1. 总共扫描 N - 1 次
  2. 对于第 $p$ 次扫描 ( $p \in [1,N-1]$ ), 将下标为 $p$ 的元素不断与其左侧元素比较，如果顺序错误就调换位置，直至到达合适的位置。
  3. 扫描完成后数列下标为 $[0,p]$ 的部分是有序的。

Lower Bound for Simple Sorting Algorithms

所有基于对于相邻元素的查找和交换的排序算法，平均时间复杂度都至少为$O(N^2)$

Binary Insertion Sort

  1. 总共扫描 N - 1 次
  2. 对于第 $p$ 次扫描 ( $p \in [1,N-1]$ ), 将下标为 $p$ 的元素在数组的 $[0,p-1]$ 范围内进行二分查找。当然查找该元素不会有结果，目的是确定需要插入的位置
  3. 将下标为 $p$ 的元素不断与其左侧元素交换直至到达 (2) 中确定的位置

Bubble Sort

  1. 总共扫描 N - 1 次
  2. 对于第 $p$ 次扫描 ( $p \in [1,N-1]$ ), 扫描的范围是 $[0,-p]$
  3. 每次扫描从左至右，对于相邻的两个元素检查顺序是否正确，并进行适当调换。
  4. 扫描完成后，数列$[-p,-1]$的部分是有序的。

这里数组的范围用了 Python 的表示方法，$[-i]$ 表示倒数第i个元素。

Shell Sort

  1. 定义一个递减的“增量序列” $h_k, h_{k-1}, \ldots, h_1$, 满足递减且 $h_1=1$
  2. 总共进行 $k$ 次以下进程：
    1. 将整个数组按增量 $h_k$ 分为 $k$ 组，组内元素下标分别满足 $0 + i_1 × h_k, 1 + i_2 × h_k, \ldots, k - 1 + i_k × h_k$.
    2. 对每一组内部的元素，在各自的位置上进行 Insertion Sort
    3. 进程结束后，每组内是有序的
  3. 第 $k$ 次进程，即增量为 1 的进程结束后，整个数列是有序的

Merge Sort

对于两个已经排序的序列 A & B, 可以各通过一次扫描将其合成为一个有序序列。

  1. 声明一个大小为 A & B 大小之和的数列 S，声明两个游标分别指向 A & B 的首个元素。
  2. 比较两个游标所指的元素，对较小的那个，放入 S 中，相应游标后移
  3. 某个已知数组中元素被完全放置后，按顺序将另一个已知数组的元素放入

归并排序的具体步骤：

  1. 将整个数列二分，对两个子数列分别递归地调用归并排序使其有序
  2. 用前述方法将两个子数列进行单次归并得到一个有序数列并返回
  3. 递归的 base case 是数列长度为 1，此时直接返回

Quick Sort

Basic Algorithm

对数列 X 进行排序:

  1. 如果 X 中的元素个数为 0 或 1，那就直接返回
  2. 确定一个 X 中的元素 v, 称之为 pivot 基准点
  3. 将 X 中除了 v 以外的元素分为比 v 小的部分 S 和比 v 大的部分 L
  4. 对 S 和 L 递归地调用 Quick sort 使其有序，并按 S, v, L 顺序返回

Median-of-Three Partitioning

将一个数列的首元素、末元素和中间元素的中位数作为 pivot.

基础算法中第 2、3 步的具体实现：（注意以下的 left, right 都是左闭右闭的，即 arr[right] 也在要排序的数组中）

  1. 确定是 arr[left], arr[right] 还是 arr[center] 是 pivot
  2. 将 pivot 与 arr[right] 交换
  3. 声明两个游标 i 和 j, 分别指向 arr[left] 和 arr[right-1]
  4. 循环以下过程，直到 j < i 为止（j < i 时不进行判断和交换）
    1. 将 i 向右移动，直到锁定某个大于 pivot 的元素
    2. 将 j 向左移动，直到锁定某个小于 pivot 的元素
    3. 交换此时的 arr[i] & arr[j]
  5. 将 arr[i] 和现在处于 arr[right] 的 pivot 交换
  6. 交换完成后 arr[i] 是 pivot, 即 Basic Algorithm 中描述的 v, 而 S 和 L 分别是对应的左右部分

Improving Median-of-Three

在寻找 median of three 的过程中，需要进行三次判断，此时就可以直接进行交换，直接使得交换后的数列中首元素 < 中间元素 < 末元素。

则此时中间元素是 pivot，且已知首元素 < pivot < 末元素, 因此在上一段 (2) 步骤中可以改为将 pivot 与 arr[right-1] 交换。i 初始化为 left + 1, j 初始化为 right - 2.

Improving Small Arrays Issue

对于小数列，快速排序可能表现比插入排序要差。

设置某个 cutoff 值，在快速排序递归到数列长度小于 cutoff 时，转而使用插入排序。

Cutoff 通常被设置为 3.

Table Sort

当某个数字只是一个 key, 连带还有很多其他数据，要根据这个 key 排序时，直接对所有的数据进行交换等是没有效率的。

此时建立另一个数列 T 来储存记录的顺序。 在排序之前，将 T 初始化为 T[i] = i. 排序完成的结果是 data[T[i]].key 从小到大有序。

排序的过程中应用前面的基础排序算法，将 arr[i] 在进行大小比较时用 data[T[i]].key 代替，交换时用 T[i] 代替。

在完成了 T 的调整，使得 data[T[i]].key 有序之后，可以高效地对所有数据本身进行物理排序。

要做到这一点，需要通过移动数据，使得数据的下标与 T “对齐”。可以证明表排序将会形成数个分离的组，各个组将会形成循环圈。按照循环圈的方向逆向转动一次就可以完成排序，如图所示。

开辟一个与数据大小相同的暂存空间，利用其对每一组循环圈进行交换，最终达成“下标与 T 对齐”, 此时 key 即有序。

Bucket Sort

默认数组 arr 中都是自然数。

  1. 需要外部信息（或进行一遍扫描），获取数列中最大元素的大小 m
  2. 声明一个大小为 m + 1 的数组 count (可访问下标最大为 m), 并且其中元素全部初始化为 0.
  3. 扫描 arr, 将 count[arr[i]] 置为 1.
  4. 从左至右扫描 count, 将每个 count[k] == 1 的 k 输出，则输出记录就是排序完成的结果。

注意如果 arr 中存在重复元素，只要将上面 (3) 修改为 count[arr[i]]++, 将 (4) 修改为将 k 输出 count[k] 次即可，这对于后面的基数排序是有重要作用的。

Radix Sort

  1. 获取数列中最高的位数 P，总共进行 P 次桶排序
  2. 每一次桶排序中，只对于某一个数位进行排序，从右到左（从个位到高位），注意入桶和出桶时按照某种玄妙的顺序

在复杂度 $O(P(N+B))$ 中，P 是最高的位数，N 是元素数量，B 是桶的数量（也就是每一位上的最大值）。

External Sorting

对于不能够直接读入内存的大数据，对其进行分块，在每个小区块完成排序之后通过归并排序的方式，直接在硬盘上合并成大块。最后合并的过程涉及到大量的硬盘 I/O.

Stability

当一个数组中存在重复的元素时，如果一个排序算法不会交换这两个元素的位置，那就称该算法为 stable, 否则为 unstable.

Stable algorithms:

  • Bubble
  • Insert
  • BST
  • Merge
  • Bucket
  • Radix

Unstable algorithms:

  • Selection
  • Shell
  • Quick
  • Pancake

Hashing

Hash Table and Hash Function

哈希表是一个固定大小 TableSize 的数组，每个 key 通过哈希函数映射到 0 到 TableSize - 1 中的某个数 i ，将 key 存在 table[i] 中。

理想情况下，哈希函数需要容易计算，并且能够保证两个不同的 key 映射到的 i 不同，也就是不产生碰撞。

可能的哈希函数选择方法：

  • 如果 key 是正整数，i = mod(key, TableSize)
    • TableSize 经常被设置为质数
    • 如果 key 的分布均匀，可以得到较好的结果
    • 可能存在 key 的分布造成结果非常差
  • 如果 key 是字符串
    1. 将所有字符的 ASCII 码相加，再对 TableSize 取模
1
2
3
4
5
6
7
8
9
10
typedef unsigned int index;

index Hash(const char * key, int TableSize){
    index hashVal = 0;
    while(*key != '\0'){
        hashVal += *key;
        key++;
    }
    return hashVal % TableSize;
}
  1. 建立一种 27 进制的方法，令 TableSize = 10007, 假设所有的字符串都有至少三位
1
2
3
index Hash(const char * key, int TableSize){
    return (key[0] + 27*key[1] + 729*key[2]) % TableSize;
}

Collision resolution

碰撞几乎是不可避免的，需要解决碰撞的策略。

Separate Chaining

对于数列中的每一个 cell, 用一个链表来保存被哈希到这个值的所有 key.

搜索某个元素时，首先通过哈希函数找到 i ，再用遍历链表的方式遍历 arr[i] 为头节点的链表。

Load factor 装填因子 $\lambda$ = number of elements / TableSize = average length of lists

Ideal $\lambda$ should approach 1.

$\lambda \ll 1$ means the table is not adequately utilized. $\lambda \gg 1$ means there are too many collisions.

However, $\lambda = 1$ itself does not mean best efficiency.

Disadvantage:

  • Allocate new cells in memory
  • Complex data structure
  • No random accessibility advantage

Open Addressing

只能在 TableSize >= Number of Elements 的时候使用。 对某个将要插入的 x, 如果发生了碰撞，就对 $h_i(x) = (\operatorname{Hash}(x) + F(i)) \operatorname{mod} \text{TableSize}$, 其中 $F(0)=0$.

Linear Probing

$F(i)=i$. 即发生碰撞后，对其对应的哈希值 +1, +2,… 进行尝试。

Quadratic Probing

$F(i)=i^2$. 具体实现见代码块：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Position Find(int key, HashTable h) {
    Position current;
    current = Hash(key, h->TableSize);
    while(h->thecells[current].info != Empty && h->thecells[current].element != key){   // While collisioning.
        current += 2*current -1;    // Explain after the code block.
        if(current >= h->TableSize){
            current = current % h->TableSize;
        }
    }
    return current;
}

void Insert(int key, HashTable H){
    Position pos = Find(key, H);
    if(H->thecells[pos].info != Legitimate){
        H->thecells[pos].info = Legitimate;
        H->thecells[pos].element = key;
    }
}

Explaining this statement:

1
current += 2*current -1

$F(i) = F(i-1) + 2 \times i - 1$ for $F(i) = i^2$. 即所用的 $F(i)$ 的递推性质。

Double Hashing

$F(i) = i \times \operatorname{Hash}_2(x)$, where $\operatorname{Hash}_2(x)$ can be arbitrarily defined.

Rehashing

如果目前的哈希表已经太满了，就可能导致运行的时间大大超出期望的 $O(1)$.

解决方案是建立另一张大约两倍大小的哈希表，并且将原哈希表中的所有元素存到新哈希表中。

Public Overflow Cache

当碰撞发生时，将新元素放入另一个公共的 overflow table.

只适用于碰撞元素数量相对较小时。

Graph Algorithms

Definitions

A graph G = (V,E) consists of a set of vertices V and a set of edges E.

Each edge is a pair $(v, w)$, where $(v, w) \in E$, and $v, w \in V$.

If the pair is ordered, then the graph is directed, called digraph. Each edge is then denoted as $<v, w>$, where $<v, w> \in E$, and $v, w \in V$.

Vertex w is adjacent to v iff. $(v, w) \in E$ or $<v, w> \in E$.

Sometimes an edge can have weight, cost, distance, etc.

Path in a graph is a sequence of vertices $w_1, w_2, \ldots, w_n$, such that $(w_i, w_{i+1} \in E)$ for $1 \leq i < n$. The length of the path is $n - 1$.

The edge from a vertex to itself is a loop.

A cycle in a digraph is a path of length at least 1 such that $w_1 = w_n$. A diagraph without cycles is acyclic, called DAG.

Connection:

  • connected - in an undirected graph, if there is a path from each vertex to any other vertex.
  • strongly connected - in a directed graph, there is a path from each vertex to any other vertex.
  • weakly connected - in a non-strongly-connected directed graph, the underlying undirected graph is connected.

In a digraph, for each edge $<v,w>$, $v$ is called the tail and $w$ is called the head.

  • Indegree: number of edges with the vertex as head
  • Outdegree: number of edges with the vertex as tail
  • Degree: the number of edges linked to the vertex.
    • Degree = Indegree + Outdegree
    • Number of edges = $\sum$ Indegree = $\sum$ Outdegree

Representation

Adjacency Matrix

一个方阵 matrix, 维度为 Vertex 的数量。

  • 有向图中， matrix[i][j] == 0 表示从 Vertex i 到 Vertex j 没有 Edge, 若为 1 表示有
  • 有权重的有向图中， matrix[i][j] 表示从 Vertex i 到 Vertex j 的权重，另外 matrix[i][j] == $\infty$ 也可以表示没有 Edge

Let $|V|$ represents the number of vertices and $|E|$ represents the number of edges, the space requirement is $O(|V|^2)$

If $|E|=O(|V|^2)$ then array implementation is appropriate, other wise the sparsity wastes space.

Adjacency List

一个数组，数组的每个元素是一个链表，链表的头节点是数组下标对应的 Vertex, 后续的节点是这个 Vertex 的 directed edge 所指向的各个 Vertex.

Degrees

  • Calculate the indegree of vertex x:
    • Adjacenct Matrix: scan matrix[x][i]
    • Adjacency List: scan the whole list
  • Calculate the outdegree of vertex x:
    • Adjacenct Matrix: scan matrix[i][x]
    • Adjacency List: scan list[x] and find how many descendant nodes are there.

Topological Sort

Definition: an ordering of vertices in a DAG, such that if there is a path from $v_i$ to $v_j$, then $v_j$ appears after $v_i$ in the ordering.

Topological ordering is NOT possible for a digraph with cycle. The ordering is NOT necessarily unique.

Preliminary Implementation

实现方案：

  1. 如果当前的图不是空的，就找到任何 Indegree == 0 的节点 v，否则就结束
  2. 输出 v, 并且将它和所有连接着它的 edge 从图中抹去，同时更新所有节点的 Indegree
  3. 重复 (1) 和 (2) 直到没有节点为止

Optimization Strategy

每次循环中，重新扫描全图并且找到 Indegree 为 0 的节点是低效的。新的符合要求的节点必然与刚刚被消除的点相邻。

利用 Queue 结构（Dequeue 后不清除记录，最终回溯整个队列获得排序）：

  1. 扫描全图获得所有节点的 Indegree 并保存
  2. Enqueue 目前所有的 0-indegree vertex
  3. Dequeue 并获得 front, 将所有 front 连接着的 vertex 的 Indegree - 1
  4. 找到新的 0-indegree vertex, Enqueue all of them
  5. 循环直到结束
  6. Queue 中的记录就是拓扑排序的结果

Shortest-Path Algorithms

两个术语：

  • BFS - Breadth First Search 广度优先
  • DFS - Depth First Search 深度优先

Unweighted Shortest Path

思路：

  1. 确定出发点 v
  2. 找到所有从 v 出发一步能够到达的点，这些点的最短路径距离为 1
  3. 将以上点作为基准，找到它们临近的点（v 除外），这些点的最短路径距离为 2
  4. 循环以上过程直到整张图被遍历

这是一种 BFS, 在过程中需要保存 3 个信息：

  1. 到 s 的距离，dist
  2. 到达这个点时作为基准的节点，path
  3. 这个点是否已经被探测过了，known

具体实现利用 Queue：

  1. Enqueue v, 其 dist = 1, path = -1 (to mark as the entrance)
  2. Dequeue 并且获取 front, 将所有 front 可以一步到达的，unknown 的点 Enqueue
  3. 循环以上过程直到所有点 Known

输出某个节点的路径时，根据 path 的值不断回溯。

Dijkstra’s Algorithm for Weighted Graph

Dijkstra’s Algorithm is a typical “Greedy Strategy”.

思路：

  1. A graph $G = (V,E)$ can be divided into 2 parts, Known and Unknown
  2. Initially, Known = {starting vertex}, $U = V -$ Known
  3. For $v \in$ Known, the shortest path is denoted as $\operatorname{Dist}(v)$
  4. The set of edges crossing Known and Unknown is denoted as $E’ = {<v,w>|v\in \operatorname{Known}, w\in \operatorname{Unknown}, <v,w> \in E}$
  5. The edge $<v’,w’>$ that can achieve the smallest $\operatorname{Dist}(v) + \operatorname{cost}(v’,w’)$ among all pairs of $<v,w>$ in $E’$ is the shortest path to vertex $w’$
  6. Update Known and Unknown
  7. Loop until the end

注意每一次循环的时候是遍历从已知部分到未知部分的所有节点对，用这对中已知节点的最短路径距离 + 两者之间的路径距离，得到未知节点从这条路到达的最短路径距离。每个未知节点在这一步中可能被包括在不同节点对中，有不同的路径距离值（通过不同的路径到达）。最终选取的是全局层面上，所有节点对给出的路径距离中最短的一个。

Critical Path Analysis

Representation

In an acyclic graph, each node represents an activity and the time it takes to complete it. The edges represent dependence relationships.

The graph is known as an activity-node graph.

Activity-Node Graph can be transformed into an Event-Node Graph.

In an event-node graph, a node represents completion of an activity, whose incoming edge represents the activity.

Dummy nodes and edges are involved to ensure the right dependencies.

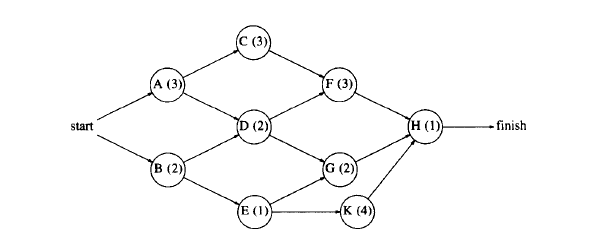
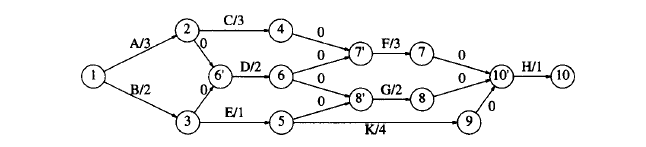
The edges that have 0 weight are dummy edges.

Dummy edges 之后跟着的节点都是 dummy nodes. 或者从另一个角度看，dummy nodes 可以由多个 edge 到达，而表示事件结束的 node 只能由 1 个 edge 到达。

Earliest Completion Time

The earliest time that a completion-node can be achieved.

$EC_i$ 表示节点 i 的 earliest completion time.

计算方法：

  1. $EC_1 = 0$
  2. $EC_w = \max(EC_v + c_{v,w})$ for all $<v,w> \in E$

Latest Completion Time

The latest completion time that each event can finish without affecting the final earliest completion time.

$LC_i$ 表示节点 i 的 latest completion time.

计算方法：

  1. 计算终点的 earlist completion time $EC_n$
  2. $LC_v = \min(LC_w - c_{v,w})$, for all $<v,w>\in E$.

从末尾节点进行倒推。

Slack Time

The amount of slack time that each completion-edge can be delayed without delaying the overall completion.

计算方法： $\operatorname{Slack}<v,w> = LC_v - EC_v$

Brief Summary

通过图片来更直观地理解：

  • 第一张图表示 Earliest Completion Time
  • 第二张图表示 Latest Completion Time
  • 两者之间的滑动（箭头）表示可以调整的空间，也即 Slack Time

All-Pairs Shortest Path

Definition: Given the non-negative directed graph, calculate the all-pairs shortest paths, from i to j for any pair <i, j> in V.

Executing |V| times Dijkstra

Executing |V| times Dijkstra’s Algorithm, each of which starts from vertex 1, 2, …, |V|.

Simple Algorithm

用 Adjacency Matrix 来表示给定的图，记为$L^{(1)}$, 矩阵中的值定义如下：

  • $L^{(1)}_{vw} = 0$ 表示 $v = w$
  • $L^{(1)}_{vw} = \text{cost/distance value of edge} <v,w>$
  • $L^{(1)}_{vw} = \infty$, 表示从 $v$ 到 $w$ 没有路径

整体而言，$L^{(1)}_{vw}$ 表示了从 $v$ 到 $w$ 在 1 步范围内的情况。

下一步，建立矩阵 $L^{(2)}$, $L^{(2)}_{vw}$ 表示从 $v$ 到 $w$ 两步之内能够达到的最短路径。

建立的规则为：$L^{(2)}{vw} = \min (L^{(1)}{vw}, L^{(1)}vx + L^{(1)}{xw}), \forall x \in V$.

具体而言，它表示从 $v$ 到 $w$ 时以节点 $x$ 作为桥梁，检查所有可能的 $x$ 找到最短路径。同时记录中介 $x$.

递推地，建立矩阵 $L^{(k)}$, $L^{(k)}_{vw}$表示的是从 $v$ 到 $w$ 经过 k 步内的最短路径。其递推式完全同理。在记录中介节点时，如果中介节点也有它的中介节点，也一并记录。即每个位置记录路径的部分都是从 $v$ 到 $w$ 的所有中间节点。

递推过程形象地表示如下，记上述的矩阵操作为 $\otimes$：

以求 $C_{23}$ 为例，则取 $L_t$ 的 Row 2 和 $L_1$ 的 Columns 3 （注意下标是从 1 开始，为了和 PPT 一致）。对荧光笔划出的四对数，分别求和$a_{21}+b_{13}, \ldots, a_{24}+b_{43}$, 取这四个和中的最小值，即为 $C_{23}$ 的值，其余元素同理。

可以证明，当 $k \geq |V| -1$ 时，$L^{(k)} = L^{(|V|-1)}$. 因此迭代计算出 $L^{(|V|-1)}$ 就可以得到最终的 all-pairs shortest path.

Optimizations
Path Storage

在存储路径时，不存储每个中间节点，而是只存储直接到达的中介节点。如果需要整条路径通过不断回溯获得。

具体实现：

  • 通过一个同样维度的矩阵 $\operatorname{Path}[i][j]$, 来记录上述的直接到达的中间节点。
  • $\operatorname{Path}[i][j] = -1$ 表示不需要中介
  • 回溯输出时，如果 $\operatorname{Path}[i][j] \neq -1$ ，则策略如下：
    1. 令 $\operatorname{Path}[i][j] = k$ 方便后续表示
    2. 输出 $k$
    3. 观察同一行的第 $k$ 列元素 $l$
      1. 若 $l = -1$, 则输出结束
      2. 若 $l \neq -1$, 则说明这是更前序的一个中介，将 $k$ 更新为 $l$，重复上一级 (2) 步骤
    4. 以上方法输出的是逆序的路径，若需要正序路径则将其反转即可
Hopping Recursion

In order to get $L^{(2k)}$, instead of obtaining $L^{(2k-1)} \otimes L^{(1)}$, we can obtain $L^{(k)} \otimes L^{(k)}$.

This decrease the numbers of matrix $\otimes$ from $|V|$ to $\log |V|$.

Local Updating

Instead of creating a new matrix to store the result of $\otimes$, update the value in the original matrix.

这样的话，在同一个矩阵空间内，分别得到的是 $L^{(1)}, L^{(2)}, L^{(4)}, \ldots, L{(2n)}$, 无法精确地得到每一步的值，但由于前述当 $k \geq |V| -1$ 时，$L^{(k)} = L^{(|V|-1)}$ 的性质，只需要迭代到 $2^n \geq |V|-1$ 就可以达到正确答案。

Floyd-Warshall Alogrithm

Definitions:

  • $D^{(0)}_{vw}$ is the shortest path with no intermediate;
  • $D^{(1)}_{vw}$ is the shortest path with intermediate vertex 1;
  • $D^{(k)}_{vw}$ is the shortest path with intermediate vertex 1, 2, …, k;

算法：$D^{(k)}{vw} = \min (D^{(k-1)}{vw}, D^{(k-1)}{vk} + D^{(k-1)}{kw})$.

理解：从 $v$ 到 $w$，以 $1,2,\ldots,k$ 为中介的最短路径，是以下两者中的最小值：

  • $D^{(k-1)}_{vw}$, 即与 $k$ 无关，$k - 1$ 时的最短路径仍然是 $k$ 时的最短路径
  • 从 $v$ 到 $k$ 的最短路径 + 从 $k$ 到 $w$ 的最短路径，两者分别可以以 $1,2,\ldots,k-1$ 为中介，即 $D^{(k-1)}{vk}+ D^{(k-1)}{kw}$

初始的 $D^{(0)}$ 为原始的路径图。

  • 0 代表 $v=w$
  • 数字代表距离
  • $\infty$ 代表从 $v$ 到 $w$ 没有直接路径

迭代直到获得 $D^{(|V|)}_{vw}$, 这是考虑了全图的最终 all-pair shortest path.

以求 $D^{(3)}$ 为例：

深蓝色与红色的数字表示框中对应的 $d_{ij}$ 元素，浅蓝色的加号表示正常的数字相加。例如 1 + 4 表示的是 $d_{31} + d_{43}$, 以此类推。

最终得到的 $e_{ij}$ 是 $D^{(2)}$ 和 $D^*$ 中 $ij$ 位置元素之间较小的值。

注意因为求的是 $D^{(3)}$, 因此选择第 3 行第 3 列，下标从 1 开始。

整个算法从 $D^{(0)}$ 出发，计算到 $D^{(4)}$，也即遍历过每一行每一列结束。

Network Flow Problem

考虑一个水流系统，“水流”从 $s$ 流向 $t$. 对于一条边 $<v,w>$, 其权重表示这条边可以经过的最大流量。

Network Flow Problem 要解决从 $s$ 流向 $t$ 的最大流量。

Simple Algorithm

对一张给定的 $G$, 画出 $G_f$ 和 $G_r$, 分别表示已经找到的流量和剩余的流量。

初始状态：

  • 两张图的节点和边的位置与原图完全相同。
  • $G_f$ 每条边的 value 为 0
  • $G_f$ 每条边的 value 与 $G$ 相同

实现过程：

  1. 在 $G_r$ 中找到任意一条从 $s$ 到 $t$ 的路径
  2. 找到这个路径上所有的边的 value 的最小值 $m$
  3. 将 $G_r$ 这条路径上的所有边的 value 减去 $m$, 将 $G_f$ 这条路径上的所有边的 value 加上 $m$
    • 注意当 $G_r$ 中有边的 value 为 0 时，就要删去这条边，不能再经过
  4. 重复以上过程，直到 $G_r$ 中没有任何可行的从 $s$ 到 $t$ 的路径为止

初始情况: (left - $G_f$, right - $G_r$)

选择完第一次路径之后的情况：

算法得到的答案不一定是正确的。

Modification

在每次从 $G_r$ 这条路径上的所有边 $<v,w>$ 的 value 减去 $m$ 时，增加一条 value 相同的 $<w,v>$ （反向）的边。

这样就能保证答案的正确性。

具体的实现可以使用 Unweighted Shortest Path 算法。

算法的复杂度为 $O(f \times |E|)$, 其中 $f$ 为最终的最大流量结果。

Minimum Spanning Tree

Consider a cost weighted graph, when asked to traverse the graph with the lowest cost, then a minimum spanning tree will be constructed.

Constructing the minimum spanning tree is to find the most cost-efficient N-1 edges to connect N verices.

Prim’s Algorithm

  • 将所有的节点划分为两个集合，其一是已经被包含在树内的 (A)，其二是未被包含在树内的 (B)。
  • 遍历从 A 到 B 的所有可能路径，将其中最短的一条路径那端的节点加入树中，这条路径作为树的连接。

本质与 Dijkstra’s Algorithm完全相同。

Kruskal’s Algorithm

解决方案：

  1. 从全局的所有边中，依次选出选中最小的边
  2. 如果这条边不会与已有的边形成回环，就将其包括入树中。否则，将其废弃
  3. 循环，直到树中的边的数量达到 $|V|-1$ 为止

PPT: Think about how to avoid a cycle. 以下是我参考资料后给出的想法，不保证正确性。

解决方案：

  1. 在建立第一条边 $e_1$ 时，建立一个集合 $S_1$, 其中元素为 $e_1$ 两侧的两个节点。
  2. 之后建立每一条边 $e$ 时，对于 $e$ 两端的节点 $v,w$：
    1. 如果 $v,w$ 都不在任意 $S_i$ 中，就新建立一个集合 $S_{n+1}$
    2. 如果 $v,w$ 中有一个在某个特定的 $S_k$ 中，另一个不在任何 $S_i$ 中，那就将这“另一个”加入 $S_k$
    3. 如果 $v,w$ 分别属于两个特定的 $S_p, S_q$, 那就合并 $S_p, S_q$
    4. 如果 $v,w$在同一个 $S_k$ 中，那么就会形成回环，这条边应当被舍弃

例如在上图中，如果下一条将要加入的边两侧的节点为：

  • 4 和 6: 合并 $S_1, S_2$
  • 4 和 2: 同属于 $S_1$ 中，此边应当废弃
  • 4 和 5: 将 5 加入 $S_1$ 中

Appendix: Table of Complexity of ALL algorithms

大类 项目 Mean/Precise Worst Best
斐波那契数列 递归 $O(\frac{5}{3}^N)$ $O(\frac{3}{2}^N)$
迭代 $O(N)$
最小子串和 穷举 $O(N^3)$
优化 $O(N^2)$
Divide-and-Conquer $O(N\log N)$
最佳 $O(N)$
查找 顺序 $O(N)$
二分 $O(\log N)$
Array Lists PrintList $O(N)$
Find $O(N)$
Findkth $O(1)$
Insert $O(N)$
Delete $O(N)$
Linked Lists PrintList $O(N)$
Find $O(N)$
Findkth $O(N)$
Insert $O(1)$
Delete $O(1)$
Linked List Implementation of Stacks IsEmpty $O(1)$
CreateStack $O(1)$
MakeEmpty $O(N)$
DisposeStack $O(N)$
Push $O(1)$
Top $O(1)$
Pop $O(1)$
Array Implementation of Stacks IsEmpty $O(1)$
CreateStack $O(1)$
MakeEmpty $O(1)$
DisposeStack $O(1)$
Push $O(1)$
Top $O(1)$
Pop $O(1)$
Array Implementation of Queue Enqueue $O(1)$
Dequeue $O(1)$
IsEmpty $O(1)$
IsFull $O(1)$
CreateQueue $O(1)$
MakeEmpty $O(1)$
DisposeQueue $O(1)$
Succ $O(1)$
Front $O(1)$
找到迷宫路径 Stacks $O(N\times M)$
Queue $O(N\times M)$
Binary Tree 四种遍历 $O(N)$
Height（函数） $O(N)$
Binary Search Tree MakeEmpty $O(N)$
Find Roughly $O(\log N)$ $O(N)$
FindMin Roughly $O(\log N)$ $O(N)$
FindMax Roughly $O(\log N)$ $O(N)$
Insert Roughly $O(\log N)$ $O(N)$
Delete Roughly $O(\log N)$ $O(N)$
Depth（层数空间复杂度） $O(\log N)$ $O(N)$ $\left\lfloor \log N\right\rfloor$
Depth after $O(N^2)$ random insert/delete $O(N^{1/2})$
Sorting BST-Based Sorting (Time) $O(N\log N)$ $O(N^2)$
BST-Based Sorting (Space) $O(N)$
Straight Selection Sort $O(N^2)$
Insertion Sort $O(N^2)$ $O(N^2)$ $O(N)$
Binary Insertion Sort $O(N^2)$ Little better than Insertion Sort Little worse than Insertion Sort
Bubble Sort $O(N^2)$ $O(N^2)$ $O(N)$
Shell Sort (General) $N/A$ $N/A$ $O(N)$
Shell Sort (1,2,4,…,$2^k$) $O(N^2)$
Shell Sort (1,3,7,…,$2^k-1$) $O(N^{3/2})$
Merge Sort (Time) $O(N\log N)$ $O(N\log N)$ $O(N\log N)$
Merge Sort (Space) $O(N)$
Quick Sort (Time) $O(N\log N)$ Detail $O(N\log N)$
Quick Sort (Space) $O(1)$
Table Sort Rearrangement $O(N)$ $3N/2$ $N+1$
Bucked Sort (Time) $O(M+N)$
Bucked Sort (Space) $O(M)$
Radix Sort (Time) explanation $O(P(N+B))$ $O(P(N+B))$
Radix Sort (Space) $O(B \times N)$
Hash Table Searching Separate Chaining explanation $1+\lambda/2$ $1+\lambda$
Adjacency Matrix Indegree $O(|V|)$
Outdegree $O(|V|)$
Adjacency List Indegree (one vertex) $O(|E|+|V|)$
Outdegree (one vertex) $O(|E|/|V|)$
InsertEdge $O(|E|/|V|)$
Indegree (whole graph) $O(|E|+|V|)$
Outdegree (whole graph) $O(|E|+|V|)$
Topological Sort Straight $O(|V|^2)$
Optimized $O(|E|+|V|)$
Critical Path Analysis Unweighted Shortest Path $O(|E|+|V|)$
Dijkstra $O(|V|^2)$
Earliest Completion Time $O(|E|+|V|)$
All-Pairs Shortest Path |V| times Dijkstra $O(|V|^3)$
Simple Matrix Iteration $O(|V|^4)$
Optimized Matrix Iteration $O(|V|^3 \log |V|)$
Floyd-Warshall $O(|V|^3)$
Network Flow Problem explanation $O(f\times |E|)$
Minimum Spanning Tree Prim $O(|V|^2)$

Detail of the worst case efficiency of Quick Sort:

对于基础算法，理论上的最差情况是 $O(N^2)$, 但是通过 Median-of-Three 等策略，可以进行规避，实际达到 $O(N\log N)$, 考试时如果遇到，会声明具体的场景。

List of Some Topics not Involved

因为我觉得不考所以跳过的一些部分：

  • Page Rank
  • B-Tree
  • Computational Complexity of External Merge Sorting
  • Pancake Sort
  • Text Pattern Matching
    • Brute Force Algorithm
    • KMP Algorithm
  • Social Network Analysis